Solutions For All Chapters – गणित Class 6
Ex 3.6 – संख्याओं का खेल
प्रश्न 1. निम्न संख्याओं का ल० (भाग विधि से) ज्ञात करें-
(i) 18, 28
हल :
ल० स० = 2 × 9 × 14 = 252
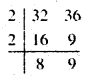
(ii) 32, 36
हल :
ल० स० = 2 × 2 × 8 × 9 = 288
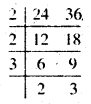
(iii) 24, 36
हल :
ल० स० = 2 × 2 × 3 × 2 × 3 = 72
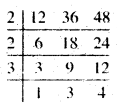
(iv) 12, 36, 48
हल :
ल० स० = 2 × 2 × 3 × 3 × 4 = 144
(v) 25, 10, 15, 45
हल :
ल० स० = 3 × 5 × 5 × 2 × 3 = 450
(vi) 8, 5
हल : ल० स० = 8 × 5 = 40
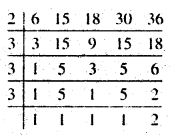
(vii) 6, 15, 18, 30, 36
हल :
ल० स० = 2 × 3 × 3 × 5 × 2 = 180
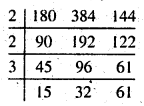
(viii) 180, 384, 144
हल :
ल० स० = 2 × 2 × 3 × 15 × 32 × 61 = 351360
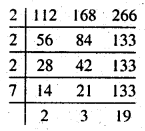
(ix) 112, 168, 266
हल :
ल० स० = 2 × 2 × 2 × 7 × 2 × 3 × 19 = 6384
(x) 240, 420, 660
हल :
ल० स० = 2 × 2 × 3 × 5 × 4 × 7 × 11 = 18480
प्रश्न 2. नीचे दिये गये प्रत्येक संख्या युग्म के लिए सिद्ध करें कि उनका गुणनफल उनके म० स० व ल० स० के गुणनफल के बराबर है-
(i) 24, 34
हल :
24 और 34 का म० स० = 2
24 और 34 का ल० स० गुणनफल = 2 × 408 = 816
म० स० और ल० स० गुणफल = 2 × 408 = 816
दी हुई संख्याओं 24 और 34 का गुणनफल = 24 × 34 = 816
अत: प्रत्येक दशा में हम देखते हैं कि म० स० और ल० स० का गुणनफल दोनों संखाओं के गुणनफल के बराबर है अर्थात्
म० स० × ल० स० = एक संख्या × दूसरी संख्या
सिद्ध हो गया।
(ii) 36, 42
हल :
36 और 42 का म० स० = 6
36 और 42 का ल० स० = 252
ल० स० और म० स० गुणफल = 252 × 6 = 1512
36 और 42 का गुणनफल = 36 × 42 = 1512
अतः प्रत्येक दशा में हम देखते हैं कि
म० स० × ल० स० = एक संख्या × दूसरी संख्या सिद्ध हो गया।
(iii) 25, 40
हल :
25 और 40 का म० स० = 5
25 और 40 का ल० स० = 200
म० स० और ल० स० गुणफल = 200 × 5 = 1000
25 और 40 का गुणनफल = 25 × 40 = 1000
अतः प्रत्येक दशा में हम देखते हैं कि
म० स० × ल० स० = एक संख्या × दूसरी संख्या सिद्ध हो गया
(iv) 15, 45
हल :
15 और 45 का म० स० = 15
15 और 45 का ल० स० = 15 × 45 = 675
म० स० और ल० स० गुणफल = 252 × 6 = 1512
15 और 45 का गुणनफल = 15 × 45 = 675
अतः प्रत्येक दशा में हम देखते हैं कि
म० स० × ल० स० = एक संख्या × दूसरी संख्या सिद्ध हो गया
प्रश्न 3. दो संख्याओं का म० स० 6 और ल० स० 36 तथा एक संख्या 18 तो दूसरी संख्या ज्ञात करें।
हल : हम जानते हैं कि एक संख्या × दूसरी संख्या = ल० स० × म० स०
6 × 36 = 18 × दूसरी संख्या
दूसरी संख्या = 6×36 /18 = 12
प्रश्न 4. दो संख्याओं का म० स० 16 और गुणनफल 6400 है। उसका ल० स० ज्ञात करें।
हल :
= 6400 /16
ल० स० = 400
प्रश्न 5. दो संख्याओं का म० स० व ल० स० क्रमशः 13 और 1989 है। यदि उनमें से एक संख्या 117 है तो दूसरी संख्या ज्ञात करें।
हल : हम जानते हैं कि एक संख्या × दूसरी संख्या = म० स० × ल० स०
117 × दूसरी संख्या = 13 × 1989
दूसरी संख्या = 13×1989 /117 = 221
अतः दूसरी संख्या = 221
प्रश्न 6. वह छोटी-से-छोटी संख्या ज्ञात करें जिसको 25, 40 और 60 से भाग करने पर 7 शेष बचे।
हल :
ल० स० = 2 × 2 × 5 × 5 × 5 × 2 × 3 = 600
अतः अभीष्ट संख्या = 600 + 7 = 607
प्रश्न 7. तीन व्यक्ति एक सुबह सैर को निकले। उनकी पग दूरी क्रमशः 80 सेमी० 85 सेमी० तथा 90 सेमी. है। ज्ञातकरें कि चलने के स्थान से कितने दूरी परउनके पग फिर एक साथ पड़ेंगे।
हल :
ल० स० = 2 × 5 × 8 × 17 × 9 = 12240
अभिष्ट दूरी = 12240 ÷ 100 = 122.4 मी० अर्थात् 122 मीटर 40 सेमी।
प्रश्न 8. 1000 के निकटतम वह संख्या ज्ञात करें जो 2, 3, 4, 5, 6 और 7 से से पूरी-पूरी विभाजित हो सके।
हल :
अतः अभीष्ट निकटतम संख्या = 10000 – 340 = 9660
या 10000 + 340 = 10340
प्रश्न 9. 1000 के निकटतम उससे बड़ी संख्या ज्ञात करें जो 8, 15 और 21 से से पूरी-पूरी विभाजित हो सके।
हल :
अतः अभीष्ट निकटतम संख्या = 10000 + (1680 – 1600) = 1000 + 80 = 10080
प्रश्न 10. एक सड़क के साथ-साथ तार के खम्भे 220 मीटर की दूरी पर लगे हैं और उसी सड़क के साथ-साथ पत्थर के ढेर 300 मीटर की समान दूरी पर लगे हैं यदि पहले ढेरी पहले खम्भे के निम्न भाग के साथ लगी हुई है तो उससे कितनी दूरी पर दूसरी ढेरी फिट खम्भे के निम्न भाग के साथ लगी होगी?
हल :
ल० स० = 2 × 2 × 5 × 5 × 11 × 3 = 3300
3300 मीटर बाद दूसरी ढेरी फिट खम्भे के निम्न भाग के साथ लगी होगी।
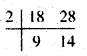




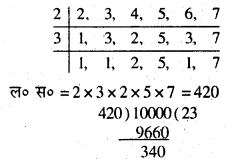
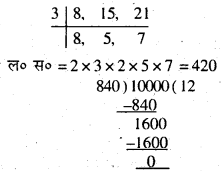


Leave a Reply