Solutions For All Chapters – गणित Class 6
Ex 3.4 – संख्याओं का खेल
प्रश्न 1. निम्न का म० स० अभाज्य गुणनखण्ड विधि से ज्ञात करें।
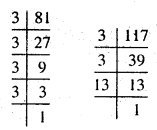
(i) 81, 117
हल :
इस प्रकार 81 = 3 × 3 × 3 × 3
117 = 3 × 3 × 13
81 और 117 में सार्व अभाज्य गुणनखण्ड = 3 × 3
महत्तम समापवर्तक = 3 × 3 = 9
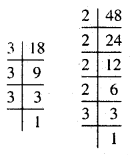
(ii) 18, 48
हल :
इस प्रकार 18 = 2 × 3 × 3
48 = 2 × 2 × 2 × 2 × 3
18 और 48 में सार्व अभाज्य गुणनखण्ड = 2 × 3
महत्तम समापवर्तक = 2 × 3 = 6
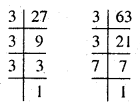
(iii) 27, 63
हल :
इस प्रकार 27 = 3 × 3 × 3
63 = 3 × 3 × 7
27 और 63 में सार्व अभाज्य गुणनखण्ड = 3 × 3
महत्तम समापवर्तक = 3 × 3 = 9
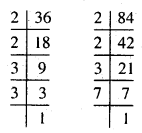
(iv) 36, 84
हल:
इस प्रकार 36 = 2 × 2 × 3 × 3
84 = 2 × 2 × 3 × 7
36 और 84 में सार्व अभाज्य गुणनखण्ड = 2 × 2 × 3
महत्तम समापवर्तक = 2 × 2 × 3 = 12
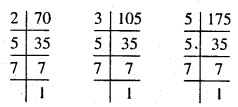
(v) 70, 105, 175
हल :
इस प्रकार 70 = 2 × 5 × 7
105 = 3 × 5 × 7
175 = 5 × 5 × 7
70, 105 और 175 में सार्व अभाज्य गुणनखण्ड = 5 × 7
महत्तम समापवर्तक = 5 × 7 = 35
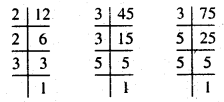
(vi) 12, 45, 75
हल :
इस प्रकार 12 = 2 × 2 × 3
45 = 3 × 3 × 5
75 = 3 × 5 × 5
12, 45 और 75 में सार्व अभाज्य गुणनखण्ड = 3
महत्तम समापवर्तक = 3
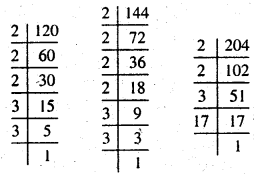
(vii) 120, 144, 204
हल :
इस प्रकार 120 = 2 × 2 × 2 × 3 × 5
144 = 2 × 2 × 2 × 2 × 3 × 3
204 = 2 × 2 × 3 × 17
120, 144 और 20 पत्तें सार्व अभाज्य गुणनखण्ड = 2 × 2 × 3
महत्तम समापवर्तक = 2 × 2 × 3 = 12
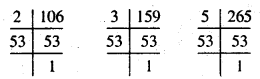
(viii) 106, 159, 265
हल :
इस प्रकार, 106 = 2 × 53
159 = 3 × 53
265 = 5 × 53
106, 159 और 265 में सार्व अभाज्य गुणनखण्ड = 53
महत्तम समापवर्तक = 53
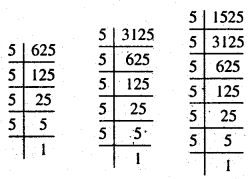
(ix) 625, 3125, 15625
हल :
इस प्रकार, 625 = 5 × 5 × 5 × 5
3125 = 5 × 5 × 5 × 5 × 5
15625 = 5 × 5 × 5 × 5 × 5 × 5
625, 3125 और 15625 में सार्व अभाज्य गुणनखण्ड = 5 × 5 × 5 × 5
महत्तम समापवर्त्तक = 5 × 5 × 5 × 5 = 625
प्रश्न 2. निम्न का म० स० भाग विधि से ज्ञात करें :
(i) 300, 450
हल :
अत: अभीष्ट म० स० = 150
(ii) 442, 1261
हल :
अतः अभीष्ट म० स० = 13
(iii) 252, 576
हल :
अतः अभीष्ट म० स० = 36
(iv) 935, 1320
हल :
अत: अभीष्ट म० स० = 55
(v) 1624, 522, 1276
हल :
अत: अभीष्ट म० स० = 58
(vi) 2241, 8217, 747
हल :
अत: अभीष्ट म० स० = 11
प्रश्न 3. 65610 विभाज्य है 27 से 65610 की दो निकटतम संख्याएँ ज्ञात करें जो 27 से विभाज्य हों।
हल :
65610 की दा निकटतम संख्याएँ जो 27 से विभाज्य हैं-
65610 – 27 तथा 65637 + 27
65583 तथा 65637
प्रश्न 4. किन्हीं दो क्रमागत संख्याओं का म० स० क्या होगा?
हल : किन्हीं दो क्रमागत संख्याओं का म० स० 1 होगा।
प्रश्न 5. दो छोटे टैंकरों में क्रमश: 85 और 68 लीटर पेट्रोल आता है उसे मापने वाने बर्तन की अधिकतम धारिता ज्ञात करें जिससे प्रत्येक टैंकर का पेट्रोल पूरा-पूरा मापा जा सके।
हल :
85 और 68 लीटर पेट्रोल मापने वाले बर्तन की अधिकतम धारिता 17 लीटर है। इससे प्रत्येक टैंकर का पेट्रोल परा- पूरा मापा जा सकता है।
प्रश्न 6. एक विद्यालय की कक्षा 6,7.8 क्रमश: 220, 116 और 132 छात्र है। इनके बराबर-बराबर बच्चे के समूह में अधिक से अधिक कितने छात्र होंगे।
हल : इनक बराबर-बराबर बच्चे के समूह में अधिक से अधिक इतने ही छात्र होंगे जो 220, 116 और 132 की पूरी तरह से विभाजित कर देता है।
अत: अभीष्ट म० स० = 220
अतः कक्षा 6, 7, 8 में क्रमश: 220, 116 और 132 छात्र हैं इनके बराबर-बराबर बच्चे के समूह में अधिक-से-अधिक 4 छात्र होंगे।
प्रश्न 7. एक आयताकार फर्श की ल० 20 मी० 16 सेमी और चौड़ाई 15 से० मी० है। इसको समान वर्गाकार टाइलें लगाकर पक्का करना है। ज्ञात करें कि इसके लिए कम-से-कम कितने टाइलें चाहिए।
हल : एक आयताकार फर्श की लं० = 20 मी० 16 मी० = 2016 सेमी
आयताकार फर्श की चौ० = 15 मी० 60 से० मी० = 1560 सेमी
अत: म० स० = 24
आयताकार फर्श को पक्का करने के लिए कम-से-कम 24 टाइलें समान वर्गाकार का चाहिए।







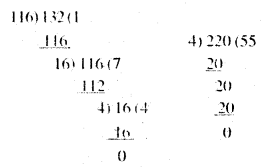


Very nice 👍 quality of questions answered
Thankuuu Google
Very easy and simple answer 😍