Trigonometric Ratio (त्रिकोणमितीय अनुपात) In Hindi
त्रिकोणमितीय अनुपात को समकोण त्रिभुज में भुजाओं के अनुपात के मान के आधार पर सभी त्रिकोणमितीय कार्यों के मान के रूप में परिभाषित किया गया है। किसी समकोण त्रिभुज की भुजाओं का उसके किसी न्यून कोण के संबंध में अनुपात उस विशेष कोण के त्रिकोणमितीय अनुपात के रूप में जाना जाता है ।
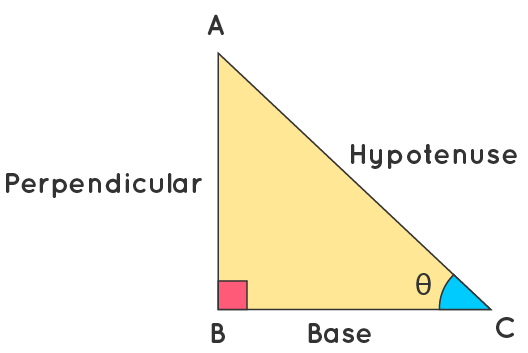
समकोण त्रिभुज की तीन भुजाएँ हैं:
1. कर्ण (सबसे लंबी भुजा)
2. लंबवत (कोण के विपरीत दिशा)
3. आधार (कोण से सटी हुई भुजा)
प्रमुख त्रिकोणमितीय अनुपात हैं:
1. साइन अनुपात (Sine Ratio)
2. कोसाइन अनुपात (Cosine Ratio)
3. टैंजेंट अनुपात (Tangent Ratio)
4. कोटेजेंट अनुपात (Cotangent Ratio)
5. सेकेंट अनुपात (Secant Ratio)
6. कोसेकेंट अनुपात (Cosecant Ratio)
Trigonometric Ratio In English
Trigonometry is all about the relationships between the angles and sides of right triangles. Trigonometric ratios, sometimes abbreviated as trig ratios, are mathematical ways to express these relationships using the ratios of the sides.
There are six main trigonometric ratios:
Sine Ratio (sin θ): The ratio of the length of the side opposite the given angle (θ) to the length of the hypotenuse.
- sin θ = Opposite Side / Hypotenuse
Cosine Ratio (cos θ): The ratio of the length of the adjacent side to the given angle (θ) to the length of the hypotenuse.
- cos θ = Adjacent Side / Hypotenuse
Tangent Ratio (tan θ): The ratio of the length of the side opposite the given angle (θ) to the length of the adjacent side.
- tan θ = Opposite / Adjacent Side
Cosecant (csc θ): The cosecant of an angle θ is equal to the reciprocal of the sine of that angle.
- sec θ = Hypotenuse/Adjacent Side
Secant (sec): The secant of an angle θ is equal to the reciprocal of the cosine of that angle.
- cosec θ = Hypotenuse/Opposite Side
Cotangent (cot): This is the reciprocal of tangent (1/tan) or the adjacent side divided by the opposite side.
- cot θ = Adjacent Side/Opposite Side
Formula
sin C = (Side opposite to ∠C)/(Hypotenuse) = AB/AC
cos C = (Side adjacent to ∠C)/(Hypotenuse) = BC/AC
tan C = (Side opposite to ∠C)/(Side adjacent to ∠C) = AB/BC = sin ∠C/cos ∠C
cosec C= 1/sin C = (Hypotenuse)/ (Side Opposite to ∠C) = AC/AB
sec C = 1/cos C = (Hypotenuse)/ (Side Opposite to ∠C) = AC/BC
cot C = 1/tan C = (Side adjacent to ∠C)/(Side opposite to ∠C)= BC/AB
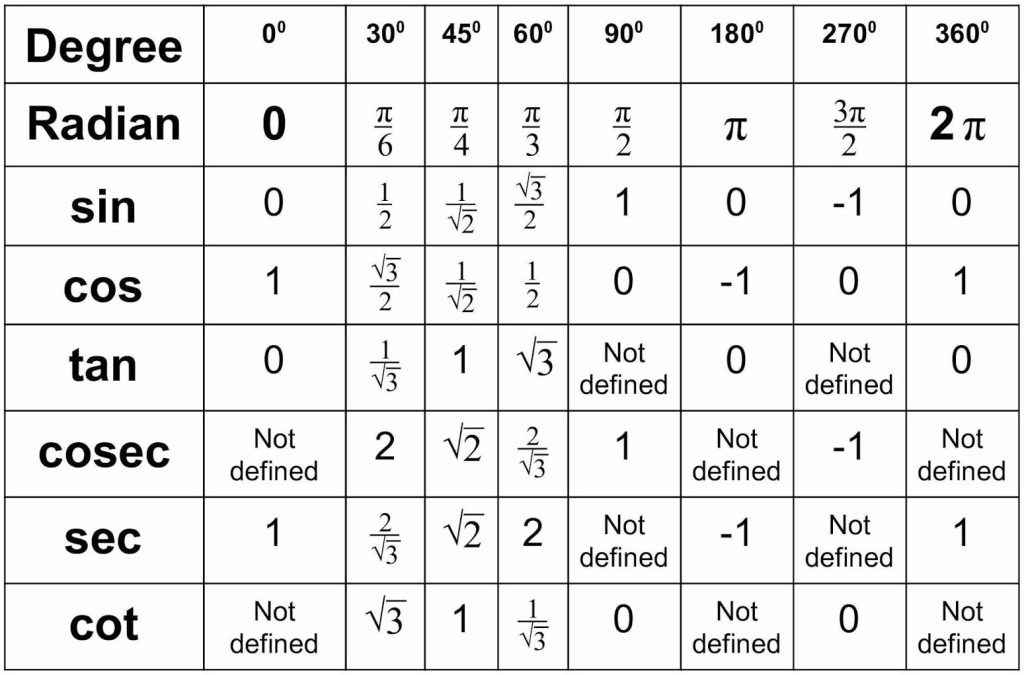
Trigonometry Table



Leave a Reply