Triangle an Its Various Kinds of Centres for Competitive Exam – Quantitative Aptitude

Triangle & Its Various Kinds of Centres (त्रिभुज और उसके विभिन्न प्रकार के केंद्र) In Hindi

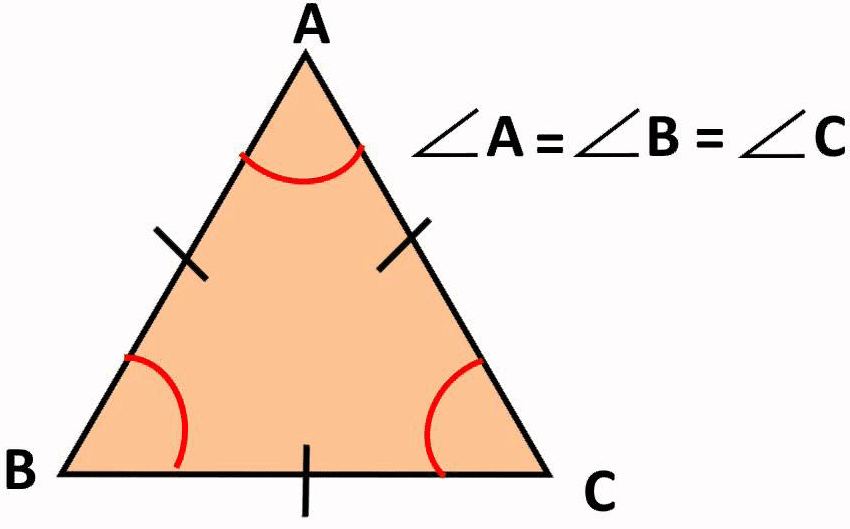
त्रिभुज एक ऐसी आकृति है जिसमें तीन भुजाएँ और तीन कोण होते हैं। यह सबसे सरल बहुभुज है। त्रिभुज के तीनों शीर्षों को A, B और C से दर्शाया जाता है और तीनों भुजाओं को AB, BC और CA से दर्शाया जाता है। त्रिभुज के तीनों कोणों को ∠A, ∠B और ∠C से दर्शाया जाता है। इसके अलावा, त्रिभुज के तीनों कोणों का योगफल हमेशा 180 डिग्री का होता है।

त्रिभुज के विभिन्न प्रकार के केंद्र:

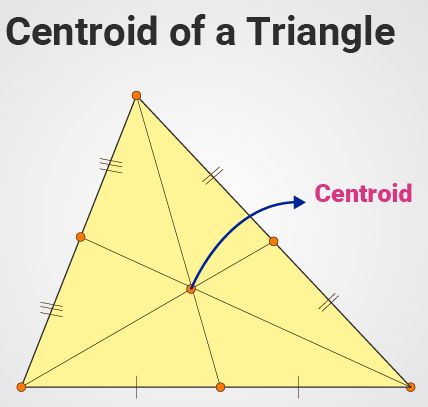
1. केंद्रक (Centroid)

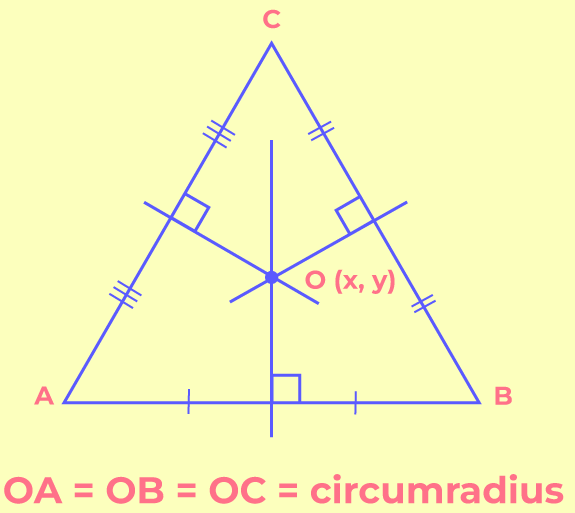
2. परिकेंद्र (Circumcenter)

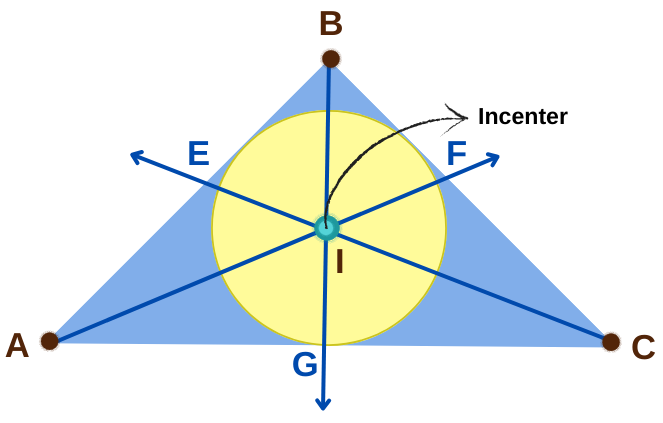
3. अंतः केंद्र (Incenter)

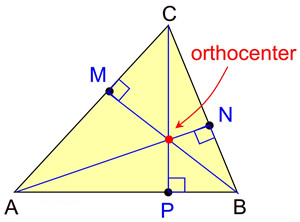
4. लम्ब केंद्र (Orthocenter)

Triangle & Its Various Kinds of Centres In English

A triangle is a polygon with three sides and three angles. It is one of the basic shapes in geometry. Triangles are characterized by three vertices (or corners) and three line segments connecting these vertices, forming three internal angles. The sum of the internal angles in a triangle is always 180 degrees. Triangles can vary in shape and size, but they always have three sides and three angles. They are fundamental geometric figures and serve as building blocks for more complex shapes and concepts in geometry.

1. Sides: A triangle has three sides, each a line segment connecting two vertices.

2. Vertices: The points where two sides meet are called vertices (plural of vertex). There are three vertices in a triangle, denoted by letters like A, B, and C.

3. Angles: Each vertex forms an angle between the two sides that meet there. A triangle has three angles, also denoted by letters like ∠A, ∠B, and ∠C.

Various Kinds of Centres:

Centroid (Center of Mass): The centroid is the point where the medians of the triangle intersect. It divides each median into two segments, with the segment closer to the vertex being twice as long as the segment closer to the midpoint of the opposite side.

Circumcenter: The circumcenter is the point where the perpendicular bisectors of the sides of the triangle intersect. It is equidistant from the three vertices of the triangle, making it the center of the circumcircle, which passes through all three vertices of the triangle.

Incenter: The incenter is the point where the angle bisectors of the interior angles of the triangle intersect. It is equidistant from the sides of the triangle, making it the center of the incircle, the circle inscribed within the triangle.

Orthocenter: The orthocenter is the point where the altitudes of the triangle intersect. An altitude is a perpendicular line segment drawn from a vertex of the triangle to the opposite side.

These four centers have significant geometric properties and relationships with the sides and angles of the triangle.