Right circular cone (दायां गोलाकार शंकु) In Hindi
Right circular cone को हिंदी में लम्बवृत्तीय शंकु कहा जाता है, यह एक त्रि-आयामी आकृति है जो एक वृत्ताकार आधार और एक सिरे पर मिलने वाली एक बिंदु शीर्ष से बनी होती है. आधार और शीर्ष को मिलाने वाला किनारा एक तरफ झुका हुआ होता है, जिसे वक्र सतह (curved surface) के रूप में जाना जाता है।
अपने दैनिक जीवन में हम विभिन्न वस्तुओं को देख सकते हैं जिनका आकर लंब वृत्ताकार शंकु जैसा होता है , जैसे आइसक्रीम कोन , जन्मदिन समारोह टोपी , वफ़ल शंकु आदि।
Right circular cone In English
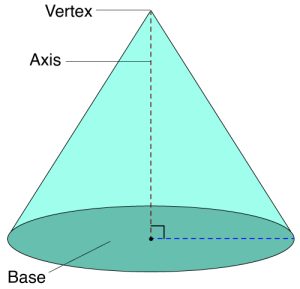
A right circular cone is a three-dimensional geometric shape that has a circular base and a curved lateral surface that tapers uniformly to a point at the top, called the apex or vertex. The axis of the cone is the imaginary line segment that runs perpendicularly from the vertex to the center of the circular base.
Parts of a Right Circular Cone
Apex (Vertex): The point at the top of the cone where all the slant heights meet. It is the opposite end of the cone from the base.
Radius (r): The radius of the cone is the distance from the center of the base to any point on the edge of the base. It’s basically the same concept of radius in a circle.
Height (h): The vertical distance from the apex (vertex) to the base. The height is perpendicular to the base.
Slant Height (l): The distance from the apex to any point on the circumference of the base. It forms the hypotenuse of a right-angled triangle along with the radius and height.
Right Circular Cone Formula
- Curved surface area = πrl
- Total surface area = π(r+l)r
- Volume = 1/3πr2h
Properties of Right Circular Cone
1. The base of the right circular cone is in a circular shape.
2. A right circular cone has one vertex.
3. Axis or line joining a vertex to the centre of the base is perpendicular to the base.
4. The slant height is the distance from the vertex to the edge of the base of the right circular cone. It is denoted by “l” or “s”
5. The altitude of the right circular cone coincides with an axis. It is denoted by h.
6. A right circular cone is formed by rotating the right-angled triangle about any one of the sides of the triangle other than the hypotenuse.


Leave a Reply