Regular Polygons (नियमित बहुभुज) In Hindi
1. बहुभुज एक समतल, द्वि-आयामी आकृति होती है जिसकी भुजाएँ सीधी होती हैं।
2. समबहुभुज एक विशेष प्रकार का बहुभुज होता है जिसकी सभी भुजाएँ लंबाई में बराबर होती हैं और सभी आंतरिक कोण माप में समान होते हैं।
Regular Polygons In English
1. A polygon is a flat, two-dimensional shape with straight sides.
2. A regular polygon is a special type of polygon where all sides are equal in length and all interior angles are equal in measure.
3. Example: A square is a polygon with made by joining 4 straight lines of equal length.
Parts of a Polygon
A polygon has three parts:
Sides: A line segment that joins two vertices is known as a side.
Vertices: The point at which two sides meet is known as a vertex.
Angles: interior and exterior. An interior angle is the angle formed within the enclosed surface of the polygon by joining the sides.
Properties of Regular Polygons
The properties of regular polygons are listed below:
1. All its sides are equal.
2. All its interior angles are equal.
3. The sum of its exterior angles is 360°.
Equilateral Triangle
An equilateral triangle is a specific type of regular polygon with three equal sides and three equal angles. It’s one of the most fundamental shapes in geometry.
Properties of an Equilateral Triangle:
1. All three sides are congruent (equal in length).
2. All three angles are congruent (equal in measure) and each angle measures 60 degrees.
3. The sum of all interior angles is 180 degrees (as with any triangle).
3. Every equilateral triangle has three lines of symmetry.
Equilateral Triangle formula
Perimeter: The perimeter P of an equilateral triangle with side length s is given by:
- P = 3s
Area: The area A of an equilateral triangle with side length s is given by:
- A = \( \frac{√3}{4} \) x \( s^2 \)
Height or Altitude: The height h (or altitude) of an equilateral triangle can be found using the formula:
- h = \( \frac{√3}{2} \) x s
Circumradius: The radius of the circumscribed circle (circumradius) R of an equilateral triangle with side length s is given by:
- R = \( \frac{s}{√3} \)
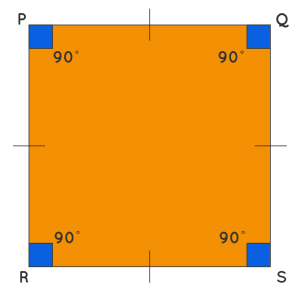
Square
A square is a regular polygon with four equal sides and four right angles (90 degrees each). It’s another fundamental geometric shape with various applications.
Properties of a Square:
1. All four sides are congruent (equal in length).
2. All four angles are congruent (equal in measure) and each is a right angle (90 degrees).
3. The sum of all interior angles is 360 degrees (as with any quadrilateral).
4. Opposite sides are parallel and congruent.
5. Diagonals of a square are perpendicular bisectors of each other (they bisect each other at a 90-degree angle and cut each other in half).
6. Each diagonal divides the square into two congruent 45-45-90 right triangles.
Square formula
Perimeter: The perimeter P of a square with side length s is given by:
- P = 4s
Area: The area A of a square with side length s is given by:
- A = \( s^2 \)
Inradius: The radius of the inscribed circle (inradius) r of a square with side length s is equal to half of the side length:
- r = \( \frac{s}{2} \)
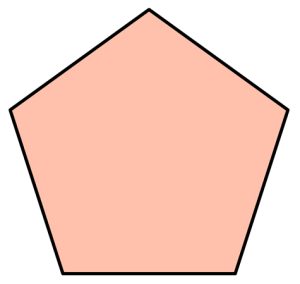
Regular Pentagon
A regular pentagon is a five-sided polygon where all sides are of equal length and all interior angles are equal in measure.
Properties of a Regular Pentagon:
1. All five sides are congruent (equal in length).
2. All five interior angles are congruent (equal in measure) and each angle measures 108 degrees.
3. The sum of all interior angles is 540 degrees (as with any pentagon).
4. Diagonals of a regular pentagon divide each other in the golden ratio (approximately 1.618).
Regular Pentagon formula
Perimeter: The perimeter P of a regular pentagon with side length s is given by:
- P = 5s
Area: The area A of a regular pentagon with side length s can be calculated using the apothem (a) and perimeter (P) as follows:
- A = \( \frac{1}{2} \) x a x P
- a = \( \frac{s}{2tan(π/5)} \)
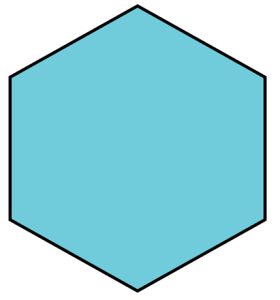
Regular Hexagon
A regular hexagon is a six-sided polygon where all sides are of equal length and all interior angles are equal in measure.
Properties of a Regular Hexagon:
1. The sum of the interior angle is 720°.
2. It has 6 equal sides.
3. It’s each interior angle is 120° and each exterior angle is 60°.
4. There are 9 diagonals and 4 triangles formed.
5. Its Perimeter is 6 x side.
Regular Hexagon formula
Perimeter: The perimeter P of a regular hexagon with side length s is given by:
- P = 6s
Area: The area A of a regular hexagon with side length s can be calculated using the apothem (a) and perimeter (P) as follows:
- A = \( \frac{3√3}{2} \) x \( s^2 \)
- a = \( \frac{s}{2} \) x √3
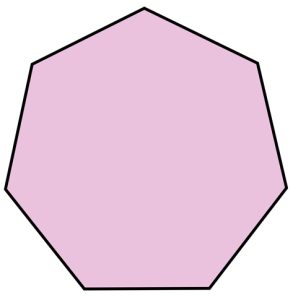
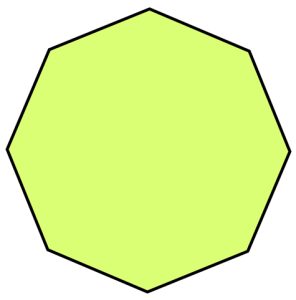
Regular Heptagon
A regular heptagon is a seven-sided polygon where all sides are of equal length and all interior angles are equal in measure.
Properties of a Regular Heptagon:
1. All seven sides are congruent (equal in length).
2. All seven interior angles are congruent (equal in measure) and each angle measures approximately 128.57 degrees.
3. The sum of all interior angles is 900 degrees (as with any heptagon).
4. Fourteen diagonals can be drawn inside a regular heptagon.
5. A regular heptagon can be inscribed in a circle, where all seven vertices lie on the circle and all sides are tangent to the circle.
Regular Heptagon formula
Perimeter: The perimeter P of a regular heptagon with side length s is given by:
- P = 7s
Area: The area A of a regular heptagon with side length s can be calculated using the apothem (a) and perimeter (P) as follows:
- A = \( \frac{7}{4} \) x \( s^2 \) x cot (\( \frac{π}{7} \))
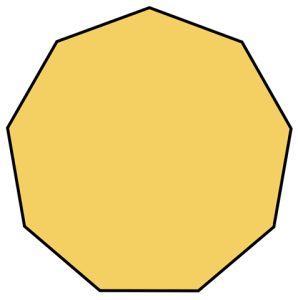
Regular Octagon
A regular octagon is an eight-sided polygon where all sides are of equal length and all interior angles are equal in measure.
Properties of a Regular Octagon:
1. The sum of the interior angle is 1080°.
2. It has 8 equal sides.
3. It’s each interior angle is 135° and each exterior angle is 45°.
4. There are 20 diagonals and 6 triangles formed.
5. Its Perimeter is 8 x side.
Regular Octagon formula
Perimeter: The perimeter P of a regular octagon with side length s is given by:
- P = 8s
Area: The area A of a regular octagon with side length s can be calculated using the apothem (a) and perimeter (P) as follows:
- A = 2(1 + √2) x \( s^2 \)
- a = \( \frac{s}{2} \) x √2(1+√2)
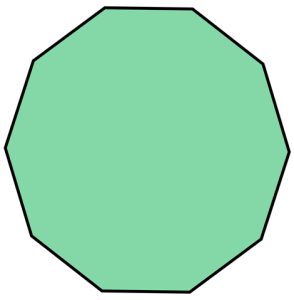
Regular Nonagon
A nonagon is a nine-sided polygon where all sides are of equal length and all interior angles are equal in measure.
Properties of a Regular Nonagon:
1. All nine sides are congruent (equal in length).
2. All nine interior angles are congruent (equal in measure) and each angle measures 140 degrees.
3. The sum of all interior angles is 1260 degrees (as with any nonagon).
4. 36 diagonals can be drawn inside a regular nonagon.
5. A regular nonagon can be inscribed in a circle, where all nine vertices lie on the circle and all sides are tangent to the circle.
Regular Nonagon formula
Perimeter: The perimeter P of a regular nonagon with side length s is given by:
- P = 9s
Area: The area A of a regular nonagon with side length s can be calculated using the apothem (a) and perimeter (P) as follows:
- A = \( \frac{9}{4} \) x \( s^2 \) x cot (\( \frac{π}{9} \))
- a = \( \frac{s}{2} \) x cot (\( \frac{π}{9} \))
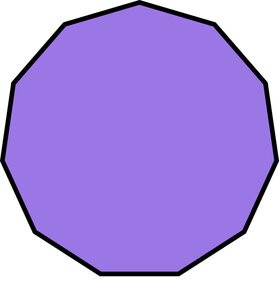
Regular Decagon
A decagon is a ten-sided polygon where all sides are of equal length and all interior angles are equal in measure.
Properties of a Regular Decagon:
1. All ten sides are congruent (equal in length).
2. All ten interior angles are congruent (equal in measure) and each angle measures 144 degrees.
3. The sum of all interior angles is 1440 degrees (as with any decagon).
4. Opposite sides are parallel and congruent.
5. It can be divided into ten congruent isosceles triangles by drawing diagonals from each vertex to the center.
6. 35 diagonals can be drawn inside a regular decagon.
7. A regular decagon can be inscribed in a circle, where all ten vertices lie on the circle and all sides are tangent to the circle.
8. A regular decagon can also be circumscribed around a circle, where all ten sides act as tangents to the circle.
Regular Decagon formula
Perimeter: The perimeter P of a regular decagon with side length s is given by:
- P = 10s
Area: The area A of a regular decagon with side length s can be calculated using the apothem (a) and perimeter (P) as follows:
- A = \( \frac{5}{2} \) x \( s^2 \) x tan (\( \frac{π}{10} \))
- a = \( \frac{s}{2} \) x tan (\( \frac{π}{10} \))
Regular Hendecagon
A hendecagon, also sometimes called an undecagon or hendecagon, is an eleven-sided polygon where all sides are of equal length and all interior angles are equal in measure.
Properties of a Regular Hendecagon:
1. All eleven sides are congruent (equal in length).
2. All eleven interior angles are congruent (equal in measure) and each angle measures approximately 147.27 degrees.
3. The sum of all interior angles is 1619.97 degrees (as with any hendecagon).
4. 55 diagonals can be drawn inside a regular hendecagon.
5. A regular hendecagon can be inscribed in a circle, where all eleven vertices lie on the circle and all sides are tangent to the circle.
Regular Hendecagon formula
Perimeter: The perimeter P of a regular hendecagon with side length s is given by:
- P = 11s
Area: The area A of a regular hendecagon with side length s can be calculated using the apothem (a) and perimeter (P) as follows:
- A = \( \frac{s}{2} \) x \( s^2 \) x cot (\( \frac{π}{11} \))
- a = \( \frac{s}{2} \) x cot (\( \frac{π}{11} \))
Regular Dodecagon
A dodecagon is a twelve-sided polygon where all sides are of equal length and all interior angles are equal in measure.
Properties of a Regular Dodecagon:
1. All twelve sides are congruent (equal in length).
2. All twelve interior angles are congruent (equal in measure) and each angle measures 150 degrees.
3. The sum of all interior angles is 1800 degrees (as with any dodecagon).
4. Opposite sides are parallel and congruent.
5. It can be divided into twelve congruent isosceles triangles by drawing diagonals from each vertex to the center.
6. 72 diagonals can be drawn inside a regular dodecagon.
7. A regular dodecagon can be inscribed in a circle, where all twelve vertices lie on the circle and all sides are tangent to the circle.
8. A regular dodecagon can also be circumscribed around a circle, where all twelve sides act as tangents to the circle.
Regular Dodecagon formula
Perimeter: The perimeter P of a regular dodecagon with side length s is given by:
- P = 12s
Area: The area A of a regular dodecagon with side length s can be calculated using the apothem (a) and perimeter (P) as follows:
- A = \( 3s^2 \) x cot (\( \frac{π}{12} \))
- A = \( \frac{s}{2} \) x cot (\( \frac{π}{12} \))





Leave a Reply