Permutation and Combination (क्रमपरिवर्तन और संयोजन) In Hindi
क्रमपरिवर्तन
क्रमपरिवर्तन, एक निश्चित क्रम में वस्तुओं को व्यवस्थित करने का तरीका है, यह गणितीय अनुप्रयोग, वस्तुओं को व्यवस्थित करने के लिए इस्तेमाल किया जाता है।
क्रमपरिवर्तन के कुछ उदाहरण
समुच्चय A = (1,6) का क्रमपरिवर्तन 2 है. जैसे कि (1,6), (6,1)।
संख्याओं के सेट = (1, 2, 3) को देखते हुए, व्यवस्था 123, 321, और 213 सेट के तीन संभावित क्रमपरिवर्तन हैं।
संयोजन
संयोजन एक सेट से वस्तुओं को चुनने का एक तरीका है जहां क्रम मायने नहीं रखता है संयोजन के साथ केवल वस्तुओं का चयन ही मायने रखता है, अर्थात् की वस्तुओं को किस क्रम में चुना गया है , यह आवश्यक नहीं है।
उदाहरण – यदि आपके पास 3 अलग-अलग रंग की शर्ट (लाल, नीला और हरा) हैं, और आप पहनने के लिए 2 चुनना चाहते हैं, तो “लाल और नीला” और “नीला और लाल” संयोजन को समान माना जाता है।
Permutation and Combination In English
Permutation
Permutation is a mathematical concept that refers to the arrangement of elements in a set, focusing on the order of those elements. In other words, it’s about how many different ways you can order a set of things.
Example – consider a set with two elements (1, 2), There are two ways, or two permutations, of arranging these elements: (1, 2) and (2, 1), The order matters, so (1, 2) is considered different from (2, 1).
Combination
A combination is a way of selecting items from a set where the order you choose them in doesn’t matter.
Example – if you have a set of three letters (A, B, C), the combinations of choosing two letters at a time without considering the order would be (A, B), (A, C), and (B, C).
Permutation and Combination Formulas
Permutations and combinations are fundamental concepts in combinatorics, the branch of mathematics concerned with counting and arranging objects.
Permutation
The permutation formula is used to calculate the number of ways to arrange a specific number of objects from a larger set, when the order of those objects matters.
Formula –
Combination
The combination formula is used to calculate the number of ways to choose a group of r objects from a set of n objects, when the order doesn’t matter.
Formula –
What is Factorial?
A factorial of a non-negative integer, denoted by n!, is the product of all positive integers less than and equal to n.
n! = n (n-1) (n-2) (n-3) (n-4) …… 3 x 2 x 1.
Example : 4! = 4 x 3 x 2 x 1 = 24
Difference Between Permutation and Combination
| Permutation | Combination |
|---|---|
| Arranging people, digits, numbers, alphabets, letters, and colours | Selection of menu, food, clothes, subjects, team. |
| Picking a team captain, pitcher and shortstop from a group. | Picking three team members from a group. |
| Picking two favourite colours, in order, from a colour brochure. | Picking two colours from a colour brochure. |
| Picking first, second and third place winners. | Picking three winners. |

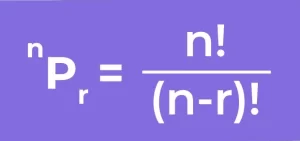
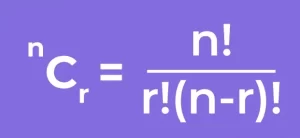


Leave a Reply