Congruence and similarity of triangles (सर्वांगसम और समरूप त्रिभुज) In Hindi
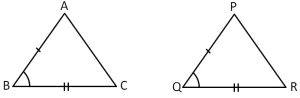
सर्वांगसम त्रिभुज
सर्वांगसम त्रिभुज वे त्रिभुज होते हैं जिनकी सभी भुजाएँ और सभी कोण क्रमशः समान होते हैं। दूसरे शब्दों में, यदि हम एक त्रिभुज को दूसरे त्रिभुज पर रखते हैं, तो वे पूरी तरह से मेल खाते हैं।
समरूप त्रिभुज
समरूप त्रिभुज वे त्रिभुज होते हैं जिनके संगत कोण समान होते हैं और संगत भुजाओं के अनुपात समान होते हैं, चाहे उन त्रिभुजों का आकार भिन्न हो।
Congruence and similarity of triangles In English
Congruence triangles
Congruent triangles are two triangles that have exactly the same size and shape. In other words, all corresponding sides are equal in length, and all corresponding angles are equal in measure. When two triangles are congruent, it means you can superimpose one triangle onto the other so that they perfectly coincide.
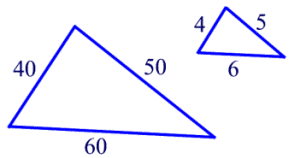
Similarity of triangles
The similarity of triangles is a geometric concept that refers to the property of having the same shape but not necessarily the same size. Two triangles are considered similar if their corresponding angles are congruent and their corresponding sides are proportional.
CPCT Full Form
The full form of CPCT is Corresponding Parts of Congruent Triangles. This is a fundamental rule used to establish equality of various parts of triangles based on their congruence.
It states that if two triangles are congruent, then each of their corresponding parts (angles and sides) are equal.
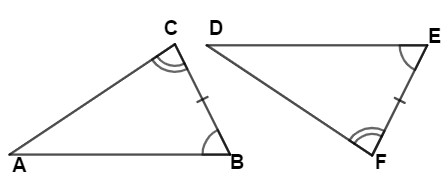
Congruence of Triangles Rules
Congruence of triangles refers to the condition when two triangles have the same size and shape. There are several rules or criteria for determining if two triangles are congruent.
1. SSS Criteria: Side-Side-Side
2. SAS Criteria: Side-Angle-Side
3. ASA Criteria: Angle-Side-Angle
4. AAS Criteria: Angle-Angle-Side
5. RHS Criteria: Right angle- Hypotenuse-Side
1. SSS (Side-Side-Side): This rule states that if all three corresponding sides of one triangle are equal in length to the corresponding sides of another triangle, then the two triangles are congruent.
AB = PQ,
BC = QR, and
CA = PR .
thus, Δ ABC ≅ Δ PQR
2. SAS (Side-Angle-Side): This rule states that if two corresponding sides and the included angle (the angle between the two sides) of one triangle are equal to the corresponding sides and included angle of another triangle, then the two triangles are congruent.
CB = RQ,
BA = QP, and
∠B = ∠Q.
thus, Δ CBA ≅ Δ RQP.
3. ASA (Angle-Side-Angle): If two corresponding angles and the included side (the side between the two angles) of one triangle are equal to the corresponding angles and included side of another triangle, then the two triangles are congruent.
BC = EF,
∠B = ∠E, and
∠C = ∠F.
thus, ΔABC ≅ ΔDEF.
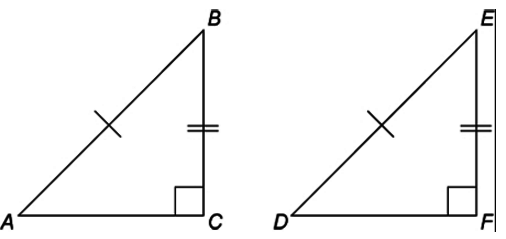
4. AAS (Angle-Angle-Side): Two triangles are congruent if two angles and a non-included side of one triangle are equal to the corresponding two angles and the non-included side of the other triangle.
AC = EF,
∠A = ∠E, and
∠B = ∠D
thus, ΔABC ≅ ΔEDF
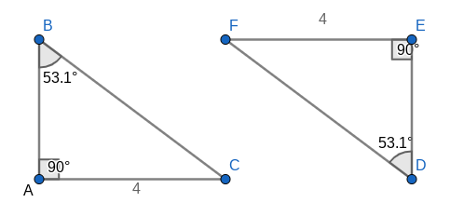
5. RHS (Right angle-Hypotenuse-Side): If the hypotenuse and a side of a right- angled triangle is equivalent to the hypotenuse and a side of the second right- angled triangle, then the two right triangles are said to be congruent by RHS rule.
∠C = ∠F (right angles)
AB = DE and
BC = EF.
thus, ΔACB ≅ ΔDFE.
Similarity of triangles Rules
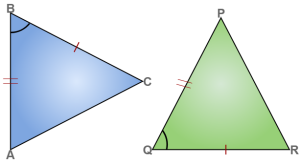
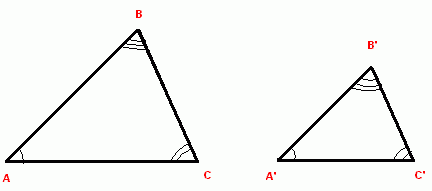
1. Angle-Angle (AA) or AAA Similarity : If two angles of one triangle are equal to two angles of another triangle, then the two triangles are similar.
<A = <A’
<C = <C’
<B = < B’
ΔABC ~ ΔA’B’C’ (AAA Similarity rule)
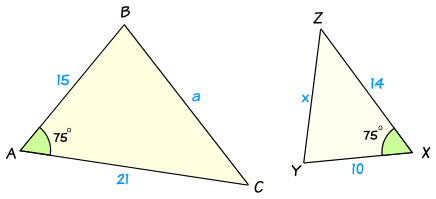
2. Side-Angle-Side (SAS) Similarity : If two sides of one triangle are proportional to two sides of another triangle, and the included angle is equal, then the two triangles are similar.
AB = PQ
<B = <Q
BC = QR
ΔABC ~ ΔPQR (SAS Similarity rule)
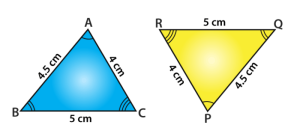
3. Side-Side-Side (SSS) Similarity : If the lengths of the corresponding sides of two triangles are proportional, then the triangles are similar.
Congruence and similarity of triangles Theorems
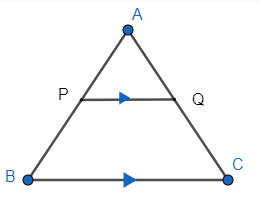
1. Basic Proportionality Theorem:
If a line is drawn parallel to one side of a triangle intersecting the other two sides at distinct points, it divides the other two sides in the same ratio.
If PQ ││ BC then,
\( \frac{AP}{PB} \) = \( \frac{AQ}{QC} \)
Example: In △ABC , PQ || BC and AP = 5cm , PB = 10cm AQ = 4cm then find the value of QC.
\( \frac{AP}{PB} \) = \( \frac{AQ}{QC} \)
Known values are AP = 5 cm, PB = 10 cm, and AQ = 4 cm. Let QC = x.
Substituting the known values and solving for x, we get:
\( \frac{5}{10} \) = \( \frac{4}{x} \)
Cross-multiplying the equation, we get:
5x = 40
x = 8
Therefore, the value of QC is 8 cm.
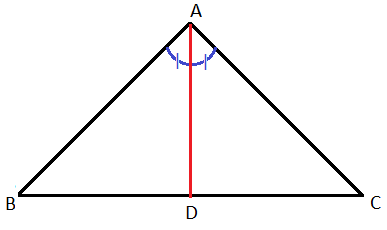
2. Angle Bisector Theorem:
The theorem states that in any triangle, the angle bisector of an angle divides the opposite side into two segments that are proportional to the lengths of the other two sides of the triangle.
If AD is bisector of <A then
\( \frac{BD}{DC} \) = \( \frac{AB}{AC} \)
Example : In △ABC , <BAD = <DAC and ab = 6cm, ac = 24cm BD = 9cm then find the value of dc.
Since we are given that <BAD = <DAC, we can be certain that triangle ABD is similar to triangle ACD by the Angle-Angle (AA) similarity postulate.
This postulate states that two triangles are similar if two corresponding angles are congruent.
\( \frac{BD}{DC} \) = \( \frac{AB}{AC} \)
Plugging in the given values:
\( \frac{9}{DC} \) = \( \frac{6}{24} \)
Solving for DC:
DC = \( \frac{(9 × 24)}{6} \)
DC = 36
Therefore, the value of DC is 36 cm.



Leave a Reply