Common tangents to two or more circles for Competitive Exam – Quantitative Aptitude

Common tangents to two or more circles(दो या दो से अधिक वृत्तों की उभयनिष्ठ स्पर्श रेखाएँ) In Hindi

Common tangents to two or more circles (दो या दो से अधिक वृत्तों की उभयनिष्ठ स्पर्श रेखाएँ) :- वह रेखा जो एक से अधिक वृत्तों पर स्पर्शरेखा होती है, उभयनिष्ठ स्पर्शरेखा कहलाती है।

यह वह रेखा होती है जो दो या दो से अधिक वृत्तों को सिर्फ एक ही बिंदु पर स्पर्श करती है। इन बिंदुओं को स्पर्श बिंदु (Sparsh बिंदु) कहा जाता है।

उभयनिष्ठ स्पर्श रेखाएं दो प्रकार की होती हैं:

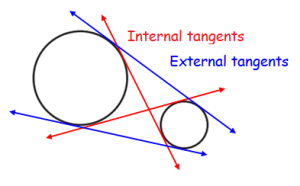
1.आंतरिक उभयनिष्ठ स्पर्श रेखा : यह वह रेखा होती है जो दोनों वृत्तों के केंद्रों के बीच से होकर गुजरती है। 2.बाह्य उभयनिष्ठ स्पर्श रेखा : यह वह रेखा होती है जो दोनों वृत्तों के केंद्रों के बीच से नहीं गुजरती है।

Common tangents to two or more circles In English

Common tangents to two or more circles :- A common tangent is a line that tangents multiple circles, generally two. Tangents can be divided into two types: internal and external tangents. External Common Tangents: These tangents lie outside both circles. If the circles do not intersect, there are two external common tangents. If the circles touch externally, there is one external common tangent. The external common tangents form a ‘V’ shape between the circles. Internal Common Tangents: These tangents lie inside both circles. If the circles do not intersect, there are two internal common tangents. If the circles touch internally, there is one internal common tangent. The internal common tangents also form a ‘V’ shape between the circles. Important facts 1.When one circle lies completely inside the other without touching, there is no common tangent. 2. When two circles touch each other internally 1 common tangent can be drawn to the circles. 3. When two circles intersect in two real and distinct points, 2 common tangents can be drawn to the circles. 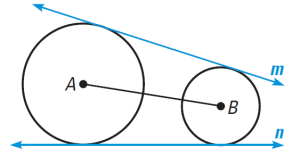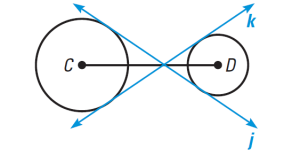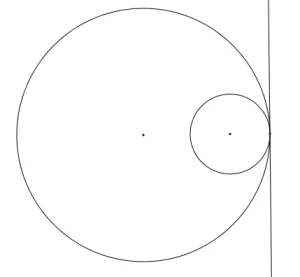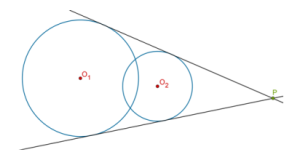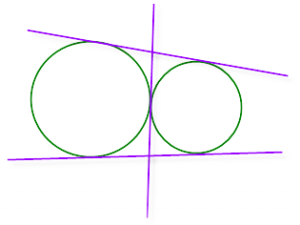4. When two circles touch each other externally, 3 common tangents can be drawn to the circles. 5. When two circle neither touch nor intersect and one lies outside the other, then 4 common tangents can be drawn. Formula

• 4 common tangents if we have r1 + r2 < C1C2
• 3 common tangents if we have r1 + r2 = C1C2
• 2 common tangents if we have |r1 – r2| < C1C2 < r1 + r2
• 1 common tangent if we have |r1 – r2| = C1C2
• no common tangents if we have C1C2 < |r1 – r2|