Question Answers विभाजन मूल्य Ch 3 Class 11 अर्थशास्त्र मराठी महाराष्ट्र

विभाजन मूल्य

प्र. १. योग्‍य पर्याय निवडा :

१) खालील विधानेचतुर्थकासाठी लागू होत नाही.

अ) प्रथम संख्या चढत्‍या किंवा उतरत्‍या क्रमाने मांडून घ्‍यावी.
ब) यात निरीक्षणाचे समान ४ भाग करता येतात.
क) ते Q१ , Q२ , Q३ असे सांकेतिक दाखवितात.
ड) Q२ हा सारणीचा मध्यगा असते.

पर्याय : १) अ २) ब आणि क
३) अ, ब आणि क ४) यापैकी नाही

उत्तर – ४) यापैकी नाही
स्पष्टीकरण: सर्व विधाने चतुर्थकासाठी लागू आहेत. चतुर्थके काढताना संख्या चढत्या किंवा उतरत्या क्रमाने मांडली जाते, निरीक्षणाचे ४ समान भाग केले जातात, ते Q₁, Q₂, Q₃ असे दर्शविले जातात आणि Q₂ हे मध्यगा असते. त्यामुळे कोणतेही विधान चतुर्थकासाठी लागू नसते असे नाही.

२) खालील सारणीचे सातवे दशमक (D७) कोणते?
सारणी – ४, ५, ६, ७, ८, ९, १०, ११, १२
पर्याय : १) ७ २) ९ ३) १० ४)१२

उत्तर – ३) १०

स्पष्टीकरण:

दशमक काढण्यासाठी सूत्र:

D₇ = 7(n + 1)/10 च्या पदाचे मूल्य

येथे n = ९ (एकूण संख्यांचा क्रम)

D₇ = 7(9 + 1)/10 = 7 × 10/10 = 7 च्या पदाचे मूल्य

चढत्या क्रमातील ७ वी संख्या = १०

∴ D₇ = १०

प्र.२. योग्य पर्यायांची जोडी ओळखा :

२) १-क, २-अ, ३-ब

स्पष्टीकरण:

चतुर्थक (Qᵢ) चे सूत्र दस्तऐवजात Qᵢ = l + (in/4 – cf)/f × h असे दिले आहे, जे पर्याय क) शी जुळते.
दशमक (Dᵢ) चे सूत्र Dᵢ = j(n + 1)/10 च्या पदाचे मूल्य असे आहे, जे पर्याय अ) शी जुळते.
शतमक (Pₖ) चे सूत्र Pₖ = l + (kn/100 – cf)/f × h असे आहे, जे पर्याय ब) शी जुळते.
∴ योग्य जोडी १-क, २-अ, ३-ब आहे.

प्र. ३. अर्थशास्त्रीय परिभाषिक शब्द सांगा :

१) समान भागांमध्येमाहितीचे/आकडेवारीचे विभाजन करण्याची प्रक्रिया….

उत्तर: विभाजन मूल्य

२) जे मूल्य दिलेल्या सामग्रीचे दहा समान भागांमध्ये विभागणी करते…

उत्तर: दशमक

३) जे मूल्य संपूर्ण निरीक्षणाचे चार समान भागांमध्ये विभागणी करते…

उत्तर: चतुर्थक

प्र. ४. खालील उदाहरणे सोडवा :

१) खालील आकडेवारी वरून पहिले चतुर्थक (Q₁), चौथे दशमक (Q4) व सव्वीसावे शतमक (P₂₅) काढा.

१८, २४, ४५, २९, ४, ७, २८, ४९, १६, २६, २५, १२, १०, ९, ८

चतुर्थक (Q₁) :

Q₁ म्हणजे १/४ व्या स्थानावर असलेली संख्या.
⇒ Q₁ चा स्थान =

$\frac{1(n+1)}{4} = \frac{1(15)}{4} = 3.75$

$4 1 ( n + 1 ) = 4 1 ( 15 ) = 3.75$

3.75 वा स्थान म्हणजे 3 व 4 व्या स्थानावरील संख्यांचा सरासरी: ⇒ 3 व 4 व्या स्थानावरील संख्या: 8 आणि 10
⇒ Q₁ =

$\frac{8 + 10}{2} = 9$

$2 8 + 10 = 9$

दशमक (D₄):

D₄ =

$\frac{4(n+1)}{10} = \frac{4 \times 15}{10} = 6$

$10 4 ( n + 1 ) = 10 4 \times 15 = 6$
⇒ 6 व्या स्थानावरील संख्या = 12
⇒ D₄ = 12

शतकम (P₂₅):

P₂₅ =

$\frac{25(n+1)}{100} = \frac{25 \times 15}{100} = 3.75$

$100 25 ( n + 1 ) = 100 25 \times 15 = 3.75$
⇒ 3 व 4 व्या स्थानावरील संख्यांची सरासरी
⇒ P₂₅ =

$\frac{8 + 10}{2} = 9$

$2 8 + 10 = 9$

२) खालील आकडेवारी वरून तिसरे चतुर्थक (Q₃), पाचवे दशमक (D₅)आणि पस्तीसावे शतमक (P₃₅) काढा.

एकूण कुटुंबसंख्या (n) = 2 + 5 + 20 + 25 + 15 + 12 = 79

संचित वारंवारता (F):

उत्पन्न (₹)	f	F
1	2	2
2	5	7
3	20	27
4	25	52
5	15	67
6	12	79

Q₃ (तिसरे चतुर्थक):

Q₃ =

$\frac{3(n+1)}{4} = \frac{3 \times 80}{4} = 60$ $4 3 ( n + 1 ) = 4 3 \times 80 = 60$

⇒ 52 < 60 ≤ 67 ⇒ Q₃ वर्ग = ₹5

L = 4.5
F = 52
f = 15
h = 1

➡ Q₃ =

$L + \frac{(60 – F)}{f} \times h$ $L + f ( 60 - F ) \times h$
➡ Q₃ =

$4.5 + \frac{8}{15} = 4.5 + 0.53 =$ $4.5 + 15 8 = 4.5 + 0.53 =$ 5.03

D₅ (पाचवे दशमक):

D₅ =

$\frac{5(n+1)}{10} = \frac{5 \times 80}{10} = 40$ $10 5 ( n + 1 ) = 10 5 \times 80 = 40$

⇒ 27 < 40 ≤ 52 ⇒ D₅ वर्ग = ₹4

L = 3.5
F = 27
f = 25
h = 1

➡ D₅ =

$3.5 + \frac{13}{25} = 3.5 + 0.52 =$ $3.5 + 25 13 = 3.5 + 0.52 =$ 4.02

P₃₅ (पस्तीसावे शतकम):

P₃₅ =

$\frac{35(n+1)}{100} = \frac{35 \times 80}{100} = 28$ $100 35 ( n + 1 ) = 100 35 \times 80 = 28$

⇒ 27 < 28 ≤ 52 ⇒ P₃₅ वर्ग = ₹4

L = 3.5
F = 27
f = 25
h = 1

➡ P₃₅ =

$3.5 + \frac{1}{25} = 3.5 + 0.04 =$ $3.5 + 25 1 = 3.5 + 0.04 =$ 3.54

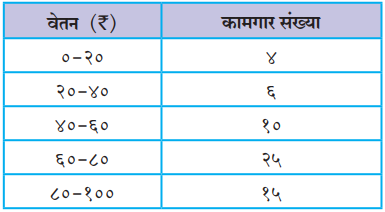
३) खालील आकडेवारी वरून पन्नासावे शतमक (P₅₀) काढा.

वेतन (₹)	f	F
0–20	4	4
20–40	6	10
40–60	10	20
60–80	25	45
80–100	15	60

पन्नासावे शतकम (P₅₀):

P₅₀ =

$\frac{50 \times 60}{100} = 30$ $100 50 \times 60 = 30$

⇒ 45 < 30 ≤ 60 ⇒ P₅₀ चा वर्ग = ₹80–100

पण… 30 हा 45 च्या आत आहे, त्यामुळे चुकीचं आहे.

खरंतर:
⇒ 20 < 30 ≤ 45 ⇒ P₅₀ चा वर्ग = ₹60–80

त्या वर्गासाठी:

L = 60
F = 20
f = 25
h = 20

गणित:

P₅₀ =

$60 + \frac{(30 – 20)}{25} \times 20$ $60 + 25 ( 30 - 20 ) \times 20$
P₅₀ =

$60 + \frac{10}{25} \times 20$ $60 + 25 10 \times 20$
P₅₀ =

$60 + 8 =$ $60 + 8 =$ ₹68

४) खालील आकडेवारी वरून तिसरे चतुर्थक (Q₃) काढा.

1. एकूण उद्योग संख्या (n):

n = 20 + 30 + 70 + 48 + 32 + 50 = 250

2. संचित वारंवारता (Cumulative Frequency):

विक्री संख्या	f	F
10–20	20	20
20–30	30	50
30–40	70	120
40–50	48	168
50–60	32	200
60–70	50	250

3. Q₃ साठी सूत्र:

Q₃ =

$L + \frac{( \frac{3n}{4} – F )}{f} \times h$ $L + f ( 4 3 n - F ) \times h$

⇒

$\frac{3 \times 250}{4} = 187.5$ $4 3 \times 250 = 187.5$

⇒ 168 < 187.5 ≤ 200 ⇒ Q₃ चा वर्ग = ₹50–60

4. घटक:

L = 50
F = 168 (या वर्गाआधीची संचित वारंवारता)
f = 32
h = 10 (वर्ग रुंदी)

5. गणित:

Q₃ =

$50 + \frac{(187.5 – 168)}{32} \times 10$ $50 + 32 ( 187.5 - 168 ) \times 10$
Q₃ =

$50 + \frac{19.5}{32} \times 10$ $50 + 32 19.5 \times 10$
Q₃ =

$50 + 6.09$ $50 + 6.09$
Q₃ = ₹56.09

५) खालील आकडेवारी वरून सातवे दशमक (D₇) काढा.

1. एकूण उद्योग संख्या (n):

n = 20 + 30 + 70 + 48 + 32 + 50 = 250

2. D₇ साठी आवश्यक मूल्य:

D₇ =

$\frac{7n}{10} = \frac{7 \times 250}{10} = 175$ $10 7 n = 10 7 \times 250 = 175$

3. संचित वारंवारता (Cumulative Frequency):

नफा (₹)	f	F
10–20	20	20
20–30	30	50
30–40	70	120
40–50	48	168
50–60	32	200
60–70	50	250

⇒ 168 < 175 ≤ 200 ⇒ D₇ चा वर्ग = ₹50–60

4. घटक:

L = 50
F = 168
f = 32
h = 10

5. सूत्र:

D₇ =

$L + \frac{( \frac{7n}{10} – F )}{f} \times h$ $L + f ( 10 7 n - F ) \times h$
D₇ =

$50 + \frac{(175 – 168)}{32} \times 10$ $50 + 32 ( 175 - 168 ) \times 10$
D₇ =

$50 + \frac{7}{32} \times 10$ $50 + 32 7 \times 10$
D₇ =

$50 + 2.19$ $50 + 2.19$
D₇ = ₹52.19

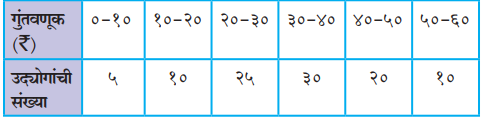
६) खालील आकडेवारी वरून पंधरावे शतमक (P₁₅) काढा.

1. एकूण उद्योगांची संख्या (n):

n = 5 + 10 + 25 + 30 + 20 + 10 = 100

2. P₁₅ साठी आवश्यक मूल्य:

P₁₅ =

$\frac{15n}{100} = \frac{15 \times 100}{100} = 15$ $100 15 n = 100 15 \times 100 = 15$

3. संचित वारंवारता (Cumulative Frequency):

गूंतवणूक (₹)	f	F
0–10	5	5
10–20	10	15
20–30	25	40
30–40	30	70
40–50	20	90
50–60	10	100

⇒ 5 < 15 ≤ 15 ⇒ P₁₅ चा वर्ग = ₹10–20

4. घटक:

L = 10
F = 5 (या वर्गाआधीची संचित वारंवारता)
f = 10
h = 10

5. सूत्र:

P₁₅ =

$L + \frac{( \frac{15n}{100} – F )}{f} \times h$ $L + f ( 100 15 n - F ) \times h$

P₁₅ =

$10 + \frac{(15 – 5)}{10} \times 10$ $10 + 10 ( 15 - 5 ) \times 10$

P₁₅ =

$10 + \frac{10}{10} \times 10 = 10 + 10$ $10 + 10 10 \times 10 = 10 + 10$

P₁₅ = ₹20

प्र. ५. खालील विधानाशी सहमत आहात की नाही ते सकारण स्पष्ट करा:

१) विभाजन मूल्यांचा वापर फक्त सैद्धांतिकदृष्ट्या केला जातो, परंतु व्यावहारिक दृष्ट्या नाही.

उत्तर: असहमत
स्पष्टीकरण: दस्तऐवजात नमूद केल्यानुसार, विभाजन मूल्यांचा (चतुर्थक, दशमक, शतमक) उपयोग व्यावहारिक क्षेत्रातही होतो. उदाहरणार्थ, आर्थिक विषमता, दारिद्र्यरेषेचे मोजमाप, रोजगारातील चढ-उतार, गुंतवणूक क्षेत्रातील कामगिरी इत्यादींच्या विश्लेषणासाठी यांचा वापर केला जातो. त्यामुळे हे केवळ सैद्धांतिक नाही तर व्यावहारिकदृष्ट्याही उपयुक्त आहे.

२) सरासरी मूल्य हे प्रातिनिधिक मूल्यांचे अयोग्य प्रतिनिधित्व करू शकते.

उत्तर: सहमत
स्पष्टीकरण: दस्तऐवजात म्हटले आहे की, जेव्हा सामग्रीमध्ये टोकाची मूल्ये (बाह्यवर्धक मूल्य) असतात, तेव्हा सरासरीने केलेले वाचन चुकीचे ठरू शकते. अशा परिस्थितीत विभाजन मूल्यांचा वापर अधिक अचूक प्रतिनिधित्वासाठी केला जातो. त्यामुळे सरासरी काहीवेळा अयोग्य प्रतिनिधित्व करू शकते हे खरे आहे.

३) ‘मध्यगेला’ ‘दुसरे चतुर्थक’ असेही म्हणतात.
उत्तर: सहमत
स्पष्टीकरण: दस्तऐवजात स्पष्टपणे नमूद आहे की दुसरे चतुर्थक (Q₂) म्हणजे मध्यगा असते. हे सूत्रांनी आणि व्याख्येनेही सिद्ध होते. त्यामुळे ‘मध्यगेला’ ‘दुसरे चतुर्थक’ असे म्हणणे योग्य आहे.

विभाजन मूल्य

प्र. १. योग्‍य पर्याय निवडा :

प्र.२. योग्य पर्यायांची जोडी ओळखा :

प्र. ३. अर्थशास्त्रीय परिभाषिक शब्द सांगा :

प्र. ४. खालील उदाहरणे सोडवा :

१) खालील आकडेवारी वरून पहिले चतुर्थक (Q₁), चौथे दशमक (Q4) व सव्वीसावे शतमक (P₂₅) काढा.

चतुर्थक (Q₁) :

दशमक (D₄):

शतकम (P₂₅):

२) खालील आकडेवारी वरून तिसरे चतुर्थक (Q₃), पाचवे दशमक (D₅)आणि पस्तीसावे शतमक (P₃₅) काढा.

एकूण कुटुंबसंख्या (n) = 2 + 5 + 20 + 25 + 15 + 12 = 79

संचित वारंवारता (F):

Q₃ (तिसरे चतुर्थक):

D₅ (पाचवे दशमक):

P₃₅ (पस्तीसावे शतकम):

३) खालील आकडेवारी वरून पन्नासावे शतमक (P₅₀) काढा.

पन्नासावे शतकम (P₅₀):

पण… 30 हा 45 च्या आत आहे, त्यामुळे चुकीचं आहे.

त्या वर्गासाठी:

गणित:

४) खालील आकडेवारी वरून तिसरे चतुर्थक (Q₃) काढा.

1. एकूण उद्योग संख्या (n):

2. संचित वारंवारता (Cumulative Frequency):

3. Q₃ साठी सूत्र:

4. घटक:

5. गणित:

५) खालील आकडेवारी वरून सातवे दशमक (D₇) काढा.

1. एकूण उद्योग संख्या (n):

2. D₇ साठी आवश्यक मूल्य:

3. संचित वारंवारता (Cumulative Frequency):

4. घटक:

5. सूत्र:

६) खालील आकडेवारी वरून पंधरावे शतमक (P₁₅) काढा.

1. एकूण उद्योगांची संख्या (n):

2. P₁₅ साठी आवश्यक मूल्य:

3. संचित वारंवारता (Cumulative Frequency):

4. घटक:

5. सूत्र:

प्र. ५. खालील विधानाशी सहमत आहात की नाही ते सकारण स्पष्ट करा:

Leave a Reply Cancel reply

CBSE Board English Medium

CBSE Board Hindi Medium

ગુજરાત બોર્ડ

PSC Exam Preparation